This article was published in the International Journal of Modern Physics D (IJMP–D) in 2007. It soon became the Top Accessed Article of the journal by Jan 2008.
Although it might seem like a hard core physics article, it is in fact an application of the philosophical insight permeating this blog and my book.
This blog version contains the abstract, introduction and conclusions. The full version of the article is available as a PDF file.
Journal Reference: IJMP-D Vol. 16, No. 6 (2007) pp. 983–1000.
.
Abstract
The softening of the GRB afterglow bears remarkable similarities to the frequency evolution in a sonic boom. At the front end of the sonic boom cone, the frequency is infinite, much like a Gamma Ray Burst (GRB). Inside the cone, the frequency rapidly decreases to infrasonic ranges and the sound source appears at two places at the same time, mimicking the double-lobed radio sources. Although a “luminal” boom violates the Lorentz invariance and is therefore forbidden, it is tempting to work out the details and compare them with existing data. This temptation is further enhanced by the observed superluminality in the celestial objects associated with radio sources and some GRBs. In this article, we calculate the temporal and spatial variation of observed frequencies from a hypothetical luminal boom and show remarkable similarity between our calculations and current observations.
Introduction
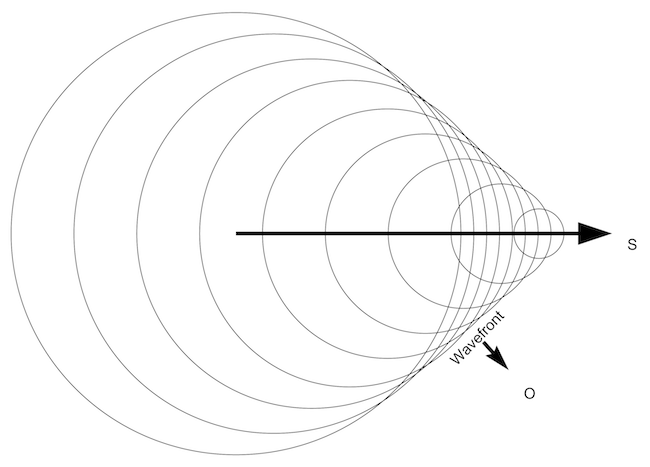
A sonic boom is created when an object emitting sound passes through the medium faster than the speed of sound in that medium. As the object traverses the medium, the sound it emits creates a conical wavefront, as shown in Figure 1. The sound frequency at this wavefront is infinite because of the Doppler shift. The frequency behind the conical wavefront drops dramatically and soon reaches the infrasonic range. This frequency evolution is remarkably similar to afterglow evolution of a gamma ray burst (GRB).
Gamma Ray Bursts are very brief, but intense flashes of  rays in the sky, lasting from a few milliseconds to several minutes, and are currently believed to emanate from cataclysmic stellar collapses. The short flashes (the prompt emissions) are followed by an afterglow of progressively softer energies. Thus, the initial
rays in the sky, lasting from a few milliseconds to several minutes, and are currently believed to emanate from cataclysmic stellar collapses. The short flashes (the prompt emissions) are followed by an afterglow of progressively softer energies. Thus, the initial  rays are promptly replaced by X-rays, light and even radio frequency waves. This softening of the spectrum has been known for quite some time, and was first described using a hypernova (fireball) model. In this model, a relativistically expanding fireball produces the
rays are promptly replaced by X-rays, light and even radio frequency waves. This softening of the spectrum has been known for quite some time, and was first described using a hypernova (fireball) model. In this model, a relativistically expanding fireball produces the  emission, and the spectrum softens as the fireball cools down. The model calculates the energy released in the
emission, and the spectrum softens as the fireball cools down. The model calculates the energy released in the 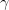 region as
region as 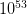 —
—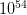 ergs in a few seconds. This energy output is similar to about 1000 times the total energy released by the sun over its entire lifetime.
ergs in a few seconds. This energy output is similar to about 1000 times the total energy released by the sun over its entire lifetime.
More recently, an inverse decay of the peak energy with varying time constant has been used to empirically fit the observed time evolution of the peak energy using a collapsar model. According to this model, GRBs are produced when the energy of highly relativistic flows in stellar collapses are dissipated, with the resulting radiation jets angled properly with respect to our line of sight. The collapsar model estimates a lower energy output because the energy release is not isotropic, but concentrated along the jets. However, the rate of the collapsar events has to be corrected for the fraction of the solid angle within which the radiation jets can appear as GRBs. GRBs are observed roughly at the rate of once a day. Thus, the expected rate of the cataclysmic events powering the GRBs is of the order of 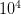 —
—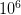 per day. Because of this inverse relationship between the rate and the estimated energy output, the total energy released per observed GRB remains the same.
per day. Because of this inverse relationship between the rate and the estimated energy output, the total energy released per observed GRB remains the same.
If we think of a GRB as an effect similar to the sonic boom in supersonic motion, the assumed cataclysmic energy requirement becomes superfluous. Another feature of our perception of supersonic object is that we hear the sound source at two different location as the same time, as illustrated in Figure 2. This curious effect takes place because the sound waves emitted at two different points in the trajectory of the supersonic object reach the observer at the same instant in time. The end result of this effect is the perception of a symmetrically receding pair of sound sources, which, in the luminal world, is a good description of symmetric radio sources (Double Radio source Associated with Galactic Nucleus or DRAGN).
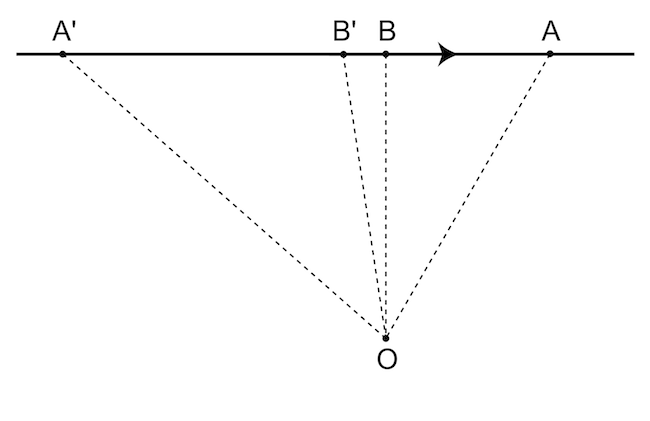
 to
to  through
through 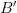 and
and 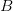 at a constant supersonic speed. Imagine that the object emits sound during its travel. The sound emitted at the point
at a constant supersonic speed. Imagine that the object emits sound during its travel. The sound emitted at the point 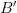 (which is near the point of closest approach
(which is near the point of closest approach 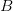 ) reaches the observer at
) reaches the observer at 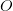 before the sound emitted earlier at
before the sound emitted earlier at 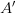 . The instant when the sound at an earlier point
. The instant when the sound at an earlier point 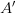 reaches the observer, the sound emitted at a much later point
reaches the observer, the sound emitted at a much later point 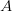 also reaches
also reaches 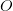 . So, the sound emitted at
. So, the sound emitted at 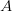 and
and 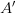 reaches the observer at the same time, giving the impression that the object is at these two points at the same time. In other words, the observer hears two objects moving away from
reaches the observer at the same time, giving the impression that the object is at these two points at the same time. In other words, the observer hears two objects moving away from 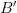 rather than one real object.
rather than one real object.Radio Sources are typically symmetric and seem associated with galactic cores, currently considered manifestations of space-time singularities or neutron stars. Different classes of such objects associated with Active Galactic Nuclei (AGN) were found in the last fifty years. Figure 3 shows the radio galaxy Cygnus A, an example of such a radio source and one of the brightest radio objects. Many of its features are common to most extragalactic radio sources: the symmetric double lobes, an indication of a core, an appearance of jets feeding the lobes and the hotspots. Some researchers have reported more detailed kinematical features, such as the proper motion of the hotspots in the lobes.
Symmetric radio sources (galactic or extragalactic) and GRBs may appear to be completely distinct phenomena. However, their cores show a similar time evolution in the peak energy, but with vastly different time constants. The spectra of GRBs rapidly evolve from 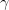 region to an optical or even RF afterglow, similar to the spectral evolution of the hotspots of a radio source as they move from the core to the lobes. Other similarities have begun to attract attention in the recent years.
region to an optical or even RF afterglow, similar to the spectral evolution of the hotspots of a radio source as they move from the core to the lobes. Other similarities have begun to attract attention in the recent years.
This article explores the similarities between a hypothetical “luminal” boom and these two astrophysical phenomena, although such a luminal boom is forbidden by the Lorentz invariance. Treating GRB as a manifestation of a hypothetical luminal boom results in a model that unifies these two phenomena and makes detailed predictions of their kinematics.

Conclusions
In this article, we looked at the spatio-temporal evolution of a supersonic object (both in its position and the sound frequency we hear). We showed that it closely resembles GRBs and DRAGNs if we were to extend the calculations to light, although a luminal boom would necessitate superluminal motion and is therefore forbidden.
This difficulty notwithstanding, we presented a unified model for Gamma Ray Bursts and jet like radio sources based on bulk superluminal motion. We showed that a single superluminal object flying across our field of vision would appear to us as the symmetric separation of two objects from a fixed core. Using this fact as the model for symmetric jets and GRBs, we explained their kinematic features quantitatively. In particular, we showed that the angle of separation of the hotspots was parabolic in time, and the redshifts of the two hotspots were almost identical to each other. Even the fact that the spectra of the hotspots are in the radio frequency region is explained by assuming hyperluminal motion and the consequent redshift of the black body radiation of a typical star. The time evolution of the black body radiation of a superluminal object is completely consistent with the softening of the spectra observed in GRBs and radio sources. In addition, our model explains why there is significant blue shift at the core regions of radio sources, why radio sources seem to be associated with optical galaxies and why GRBs appear at random points with no advance indication of their impending appearance.
Although it does not address the energetics issues (the origin of superluminality), our model presents an intriguing option based on how we would perceive hypothetical superluminal motion. We presented a set of predictions and compared them to existing data from DRAGNs and GRBs. The features such as the blueness of the core, symmetry of the lobes, the transient 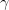 and X-Ray bursts, the measured evolution of the spectra along the jet all find natural and simple explanations in this model as perceptual effects. Encouraged by this initial success, we may accept our model based on luminal boom as a working model for these astrophysical phenomena.
and X-Ray bursts, the measured evolution of the spectra along the jet all find natural and simple explanations in this model as perceptual effects. Encouraged by this initial success, we may accept our model based on luminal boom as a working model for these astrophysical phenomena.
It has to be emphasized that perceptual effects can masquerade as apparent violations of traditional physics. An example of such an effect is the apparent superluminal motion, which was explained and anticipated within the context of the special theory of relativity even before it was actually observed. Although the observation of superluminal motion was the starting point behind the work presented in this article, it is by no means an indication of the validity of our model. The similarity between a sonic boom and a hypothetical luminal boom in spatio-temporal and spectral evolution is presented here as a curious, albeit probably unsound, foundation for our model.
One can, however, argue that the special theory of relativity (SR) does not deal with superluminality and, therefore, superluminal motion and luminal booms are not inconsistent with SR. As evidenced by the opening statements of Einstein’s original paper, the primary motivation for SR is a covariant formulation of Maxwell’s equations, which requires a coordinate transformation derived based partly on light travel time (LTT) effects, and partly on the assumption that light travels at the same speed with respect to all inertial frames. Despite this dependence on LTT, the LTT effects are currently assumed to apply on a space-time that obeys SR. SR is a redefinition of space and time (or, more generally, reality) in order to accommodate its two basic postulates. It may be that there is a deeper structure to space-time, of which SR is only our perception, filtered through the LTT effects. By treating them as an optical illusion to be applied on a space-time that obeys SR, we may be double counting them. We may avoid the double counting by disentangling the covariance of Maxwell’s equations from the coordinate transformations part of SR. Treating the LTT effects separately (without attributing their consequences to the basic nature of space and time), we can accommodate superluminality and obtain elegant explanations of the astrophysical phenomena described in this article. Our unified explanation for GRBs and symmetric radio sources, therefore, has implications as far reaching as our basic understanding of the nature of space and time.
Photo by NASA Goddard Photo and Video 

