This unpublished article is a sequel to my earlier paper (also posted here as “Are Radio Sources and Gamma Ray Bursts Luminal Booms?“). This blog version contains the abstract, introduction and conclusions. The full version of the article is available as a PDF file.

.

Abstract

Light travel time effects (LTT) are an optical manifestation of the finite speed of light. They can also be considered perceptual constraints to the cognitive picture of space and time. Based on this interpretation of LTT effects, we recently presented a new hypothetical model for the temporal and spatial variation of the spectrum of Gamma Ray Bursts (GRB) and radio sources. In this article, we take the analysis further and show that LTT effects can provide a good framework to describe such cosmological features as the redshift observation of an expanding universe, and the cosmic microwave background radiation. The unification of these seemingly distinct phenomena at vastly different length and time scales, along with its conceptual simplicity, can be regarded as indicators of the curious usefulness of this framework, if not its validity.

Introduction

The finite speed of light plays an important part in how we perceive distance and speed. This fact should hardly come as a surprise because we do know that things are not as we see them. The sun that we see, for instance, is already eight minutes old by the time we see it. This delay is trivial; if we want to know what is going on at the sun now, all we have to do is to wait for eight minutes. We, nonetheless, have to “correct” for this distortion in our perception due to the finite speed of light before we can trust what we see.

What is surprising (and seldom highlighted) is that when it comes to sensing motion, we cannot back-calculate the same way we take out the delay in seeing the sun. If we see a celestial body moving at an improbably high speed, we cannot figure out how fast and in what direction it is “really” moving without making further assumptions. One way of handling this difficulty is to ascribe the distortions in our perception of motion to the fundamental properties of the arena of physics — space and time. Another course of action is to accept the disconnection between our perception and the underlying “reality” and deal with it in some way.

Exploring the second option, we assume an underlying reality that gives rise to our perceived picture. We further model this underlying reality as obeying classical mechanics, and work out our perceived picture through the apparatus of perception. In other words, we do not attribute the manifestations of the finite speed of light to the properties of the underlying reality. Instead, we work out our perceived picture that this model predicts and verify whether the properties we do observe can originate from this perceptual constraint.

Space, the objects in it, and their motion are, by and large, the product of optical perception. One tends to take it for granted that perception arises from reality as one perceives it. In this article, we take the position that what we perceive is an incomplete or distorted picture of an underlying reality. Further, we are trying out classical mechanics for the the underlying reality (for which we use terms like absolute, noumenal or physical reality) that does cause our perception to see if it fits with our perceived picture (which we may refer to as sensed or phenomenal reality).

Note that we are not implying that the manifestations of perception are mere delusions. They are not; they are indeed part of our sensed reality because reality is an end result of perception. This insight may be behind Goethe’s famous statement, “Optical illusion is optical truth.”

We applied this line of thinking to a physics problem recently. We looked at the spectral evolution of a GRB and found it to be remarkably similar to that in a sonic boom. Using this fact, we presented a model for GRB as our perception of a “luminal” boom, with the understanding that it is our perceived picture of reality that obeys Lorentz invariance and our model for the underlying reality (causing the perceived picture) may violate relativistic physics. The striking agreement between the model and the observed features, however, extended beyond GRBs to symmetric radio sources, which can also be regarded as perceptual effects of hypothetical luminal booms.

In this article, we look at other implications of the model. We start with the similarities between the light travel time (LTT) effects and the coordinate transformation in Special Relativity (SR). These similarities are hardly surprising because SR is derived partly based on LTT effects. We then propose an interpretation of SR as a formalization of LTT effects and study a few observed cosmological phenomena in the light of this interpretation.

Similarities between Light Travel Time Effects and SR

Special relativity seeks a linear coordinate transformation between coordinate systems in motion with respect to each other. We can trace the origin of linearity to a hidden assumption on the nature of space and time built into SR, as stated by Einstein: “In the first place it is clear that the equations must be linear on account of the properties of homogeneity which we attribute to space and time.” Because of this assumption of linearity, the original derivation of the transformation equations ignores the asymmetry between approaching and receding objects. Both approaching and receding objects can be described by two coordinate systems that are always receding from each other. For instance, if a system 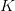is moving with respect to another system 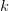along the positive X axis of 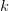, then an object at rest in 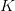at a positive is receding while another object at a negative is approaching an observer at the origin of .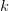

The coordinate transformation in Einstein’s original paper is derived, in part, a manifestation of the light travel time (LTT) effects and the consequence of imposing the constancy of light speed in all inertial frames. This is most obvious in the first thought experiment, where observers moving with a rod find their clocks not synchronized due to the difference in light travel times along the length of the rod. However, in the current interpretation of SR, the coordinate transformation is considered a basic property of space and time.

One difficulty that arises from this interpretation of SR is that the definition of the relative velocity between the two inertial frames becomes ambiguous. If it is the velocity of the moving frame as measured by the observer, then the observed superluminal motion in radio jets starting from the core region becomes a violation of SR. If it is a velocity that we have to deduce by considering LT effects, then we have to employ the extra ad-hoc assumption that superluminality is forbidden. These difficulties suggest that it may be better to disentangle the light travel time effects from the rest of SR.

In this section, we will consider space and time as a part of the cognitive model created by the brain, and argue that special relativity applies to the cognitive model. The absolute reality (of which the SR-like space-time is our perception) does not have to obey the restrictions of SR. In particular, objects are not restricted to subluminal speeds, but they may appear to us as though they are restricted to subluminal speeds in our perception of space and time. If we disentangle LTT effects from the rest of SR, we can understand a wide array of phenomena, as we shall see in this article.

Unlike SR, considerations based on LTT effects result in intrinsically different set of transformation laws for objects approaching an observer and those receding from him. More generally, the transformation depends on the angle between the velocity of the object and the observer’s line of sight. Since the transformation equations based on LTT effects treat approaching and receding objects asymmetrically, they provide a natural solution to the twin paradox, for instance.

Conclusions

Because space and time are a part of a reality created out of light inputs to our eyes, some of their properties are manifestations of LTT effects, especially on our perception of motion. The absolute, physical reality presumably generating the light inputs does not have to obey the properties we ascribe to our perceived space and time.

We showed that LTT effects are qualitatively identical to those of SR, noting that SR only considers frames of reference receding from each other. This similarity is not surprising because the coordinate transformation in SR is derived based partly on LTT effects, and partly on the assumption that light travels at the same speed with respect to all inertial frames. In treating it as a manifestation of LTT, we did not address the primary motivation of SR, which is a covariant formulation of Maxwell’s equations. It may be possible to disentangle the covariance of electrodynamics from the coordinate transformation, although it is not attempted in this article.

Unlike SR, LTT effects are asymmetric. This asymmetry provides a resolution to the twin paradox and an interpretation of the assumed causality violations associated with superluminality. Furthermore, the perception of superluminality is modulated by LTT effects, and explains 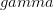ray bursts and symmetric jets. As we showed in the article, perception of superluminal motion also holds an explanation for cosmological phenomena like the expansion of the universe and cosmic microwave background radiation. LTT effects should be considered as a fundamental constraint in our perception, and consequently in physics, rather than as a convenient explanation for isolated phenomena.

Given that our perception is filtered through LTT effects, we have to deconvolute them from our perceived reality in order to understand the nature of the absolute, physical reality. This deconvolution, however, results in multiple solutions. Thus, the absolute, physical reality is beyond our grasp, and any assumed properties of the absolute reality can only be validated through how well the resultant perceived reality agrees with our observations. In this article, we assumed that the underlying reality obeys our intuitively obvious classical mechanics and asked the question how such a reality would be perceived when filtered through light travel time effects. We demonstrated that this particular treatment could explain certain astrophysical and cosmological phenomena that we observe.

The coordinate transformation in SR can be viewed as a redefinition of space and time (or, more generally, reality) in order to accommodate the distortions in our perception of motion due to light travel time effects. One may be tempted to argue that SR applies to the “real” space and time, not our perception. This line of argument begs the question, what is real? Reality is only a cognitive model created in our brain starting from our sensory inputs, visual inputs being the most significant. Space itself is a part of this cognitive model. The properties of space are a mapping of the constraints of our perception.

The choice of accepting our perception as a true image of reality and redefining space and time as described in special relativity indeed amounts to a philosophical choice. The alternative presented in the article is inspired by the view in modern neuroscience that reality is a cognitive model in the brain based on our sensory inputs. Adopting this alternative reduces us to guessing the nature of the absolute reality and comparing its predicted projection to our real perception. It may simplify and elucidate some theories in physics and explain some puzzling phenomena in our universe. However, this option is yet another philosophical stance against the unknowable absolute reality.