This post uses Easy LaTeX Pro to display equations.
Lorentz transformation is a rotation in the Minkowski space. In order to see it, let’s first look at rotation in Euclidean space, which can be written as X’ = R X. In the 2-D case, the matrix of rotation R is,
![\left[ {\begin{array}{*{20}c}{\cos \theta } & { - \sin \theta } \\{\sin \theta } & {\cos \theta } \\\end{array}} \right]](https://www.thulasidas.com/wp-content/uploads/easy-latex-cache/tex_28608e534620784ecd3b08d6a6253fbb.png "\left[ {\begin{array}{*{20}c}{\cos \theta } & { - \sin \theta } \\{\sin \theta } & {\cos \theta } \\\end{array}} \right]")
So, the matrix equation expands to
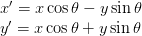
where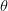 
is the angle of rotation. This is how a point 
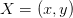in the original frame transforms to 
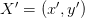in the rotated frame.
Similarly, LT in Minkowski space is X’ = L X. Lorentz Transformation matrix (in our 2-D case) is,
![\left[ {\begin{array}{*{20}c}\gamma & { - \beta \gamma } \\{ - \beta \gamma } & \gamma \\\end{array}} \right]](https://www.thulasidas.com/wp-content/uploads/easy-latex-cache/tex_9a7d0189f9911a3726f096d08aa3e9dc.png "\left[ {\begin{array}{*{20}c}\gamma & { - \beta \gamma } \\{ - \beta \gamma } & \gamma \\\end{array}} \right]")
where 
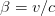and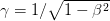 
This expands to
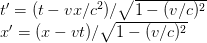
Note that rotation (and so LT) is a linear transformation, which means that the matrix R (or L) has to be independent of the vector it transforms. What happens when the matrix is a function of x, y or t? The geometry becomes non-flat and the metric tensor we defined doesn’t define the invariant distance any longer. The geometry requires a different metric tensor. Therefore, rotation or LT as we defined it and the associated single component equations is not valid any more. I will illustrate it further using 2-D rotation in the next post and show what they mean when they say that space-time is curved.
2 thoughts on “Of Rotation, LT and Acceleration”
Comments are closed.